Generating Platonic Solids in C++

Jan 03, 2021

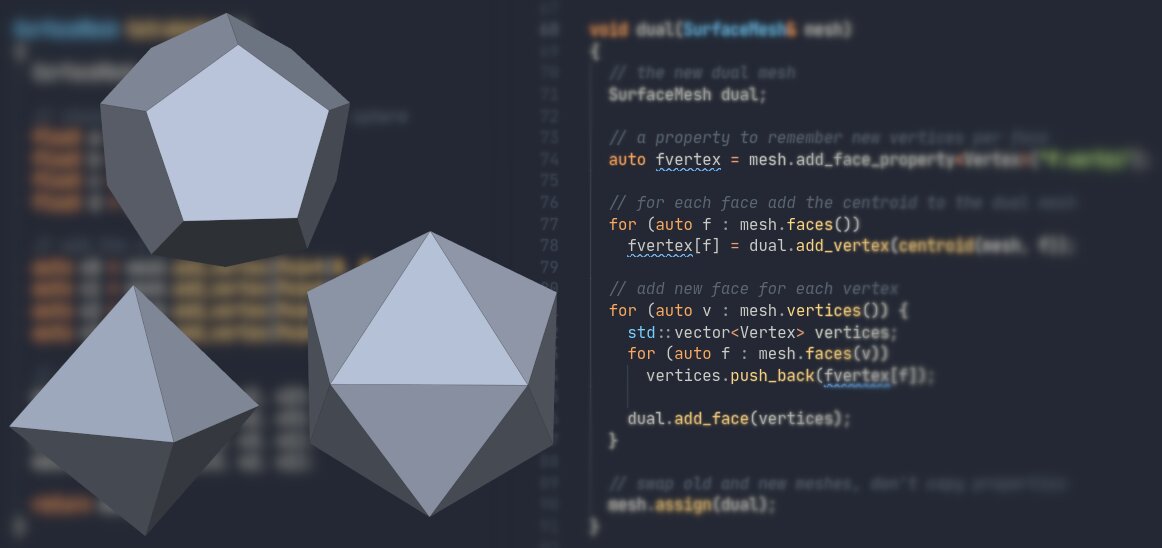
Platonic solids in front of blurry C++ code

This is a short tutorial on generating polygonal surface meshes of the five Platonic solids in C++. You can learn a few basics of working with meshes along the way. I’m using the Polygon Mesh Processing Library for implementation. The code is straightforward, so you can easily adapt it to another data structure or programming language.

Motivation

My primary motivation for this article is very simple:

You want to generate a mesh of a Platonic solid
Here is some straightforward C++ code to do so

Now why exactly would this be interesting? Well, having the possibility to generate a mesh with known properties is useful in many situations. Here are three examples:

Generating example data for an algorithm you are developing
Generating shapes in your application without shipping meshes
Unit testing geometric algorithms

Generating simple shapes also is a canonical example for doing your first steps using a mesh library, a sort of “Hello, mesh!”. If you are new to working with meshes, this is a great starting point to get familiar with the basics.

Bootstrapping

I’m using the Polygon Mesh Processing Library (PMP) as mesh data structure in this tutorial. However, any modern mesh data structure providing basic functions such as adding vertices and polygonal faces should be sufficient for this tutorial. Skip this section if you’re using another data structure.

If you want to quickly visualize the resulting meshes, I recommend downloading and compiling the PMP project template, which contains a ready-to-use mesh viewer. Just clone the repository:

git clone --recursive https://github.com/pmp-library/pmp-template.git

Build the project:

cd pmp-template && mkdir build && cd build && cmake .. && make

Run the viewer:

./myviewer

During this tutorial, I’ll define a few functions to generate the different shapes. It’s easiest to add those functions to the MyViewer class and call them on a keyboard shortcut. Here’s how to do this:

Find the MyViewer::keyboard() function in your favorite IDE
Add a new case label such as GLFW_KEY_G to the switch statement
Add the function you want to call
Add a call to update_mesh() to update the viewer
Re-compile and run ./myviewer

That’s all you need to get started, so let’s go!

The Five Platonic Solids

The Platonic solids are a set of well-known convex polyhedra with particular properties, e.g., all faces are of the same type, the faces are regular (all angles and sides are the same), and the same number of faces are incident to each vertex. In 3D space, there are only five polyhedra satisfying these criteria: The tetrahedron, hexahedron, octahedron, dodecahedron, and the icosahedron. Here they are, from left to right:

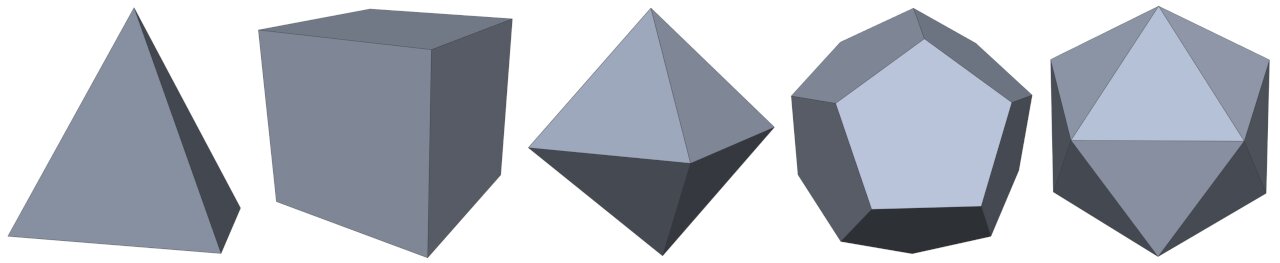
The five Platonic solids

The Platonic solids date back to the time of the ancient Greeks, if not earlier. They played a key role in Plato’s philosophy, hence the name. If you are interested, see the Wikipedia article for more information.

The Tetrahedron

Let’s begin with the simplest Platonic solid, the tetrahedron. Four vertices and four triangular faces, that’s all. Here’s the code:

SurfaceMesh tetrahedron()
{
  SurfaceMesh mesh;

  // choose coordinates on the unit sphere
  float a = 1.0f / 3.0f;
  float b = sqrt(8.0f / 9.0f);
  float c = sqrt(2.0f / 9.0f);
  float d = sqrt(2.0f / 3.0f);

  // add the 4 vertices
  auto v0 = mesh.add_vertex(Point(0, 0, 1));
  auto v1 = mesh.add_vertex(Point(-c, d, -a));
  auto v2 = mesh.add_vertex(Point(-c, -d, -a));
  auto v3 = mesh.add_vertex(Point(b, 0, -a));

  // add the 4 faces
  mesh.add_triangle(v0, v1, v2);
  mesh.add_triangle(v0, v2, v3);
  mesh.add_triangle(v0, v3, v1);
  mesh.add_triangle(v3, v2, v1);

  return mesh;
}

The Hexahedron

The code for the hexahedron isn’t that much more complicated. You just have to add a few more points and faces: Eight vertices, six quadrilateral faces:

SurfaceMesh hexahedron()
{
  SurfaceMesh mesh;

  // choose coordinates on the unit sphere
  float a = 1.0f / sqrt(3.0f);

  // add the 8 vertices
  auto v0 = mesh.add_vertex(Point(-a, -a, -a));
  auto v1 = mesh.add_vertex(Point(a, -a, -a));
  auto v2 = mesh.add_vertex(Point(a, a, -a));
  auto v3 = mesh.add_vertex(Point(-a, a, -a));
  auto v4 = mesh.add_vertex(Point(-a, -a, a));
  auto v5 = mesh.add_vertex(Point(a, -a, a));
  auto v6 = mesh.add_vertex(Point(a, a, a));
  auto v7 = mesh.add_vertex(Point(-a, a, a));

  // add the 6 faces
  mesh.add_quad(v3, v2, v1, v0);
  mesh.add_quad(v2, v6, v5, v1);
  mesh.add_quad(v5, v6, v7, v4);
  mesh.add_quad(v0, v4, v7, v3);
  mesh.add_quad(v3, v7, v6, v2);
  mesh.add_quad(v1, v5, v4, v0);

  return mesh;
}

The next shape in the series is the octahedron. You could do exactly the same as above and manually specify all vertex coordinates and face indices. However, this becomes tedious rather quickly.

Instead, you can do something slightly more intelligent and exploit the fact that every convex polyhedron has a dual polyhedron.

Interlude: Computing the Dual Polyhedron

The dual polyhedron is a bit like a twin—or maybe it is more like Dr. Jekyll and Mr. Hyde? I’ll leave it up to you. Here’s the slightly more formal definition: For each convex polyhedron, there is a dual polyhedron with a face for each vertex and a vertex for each face of the original polyhedron. Here’s an illustration of the concept of duality:

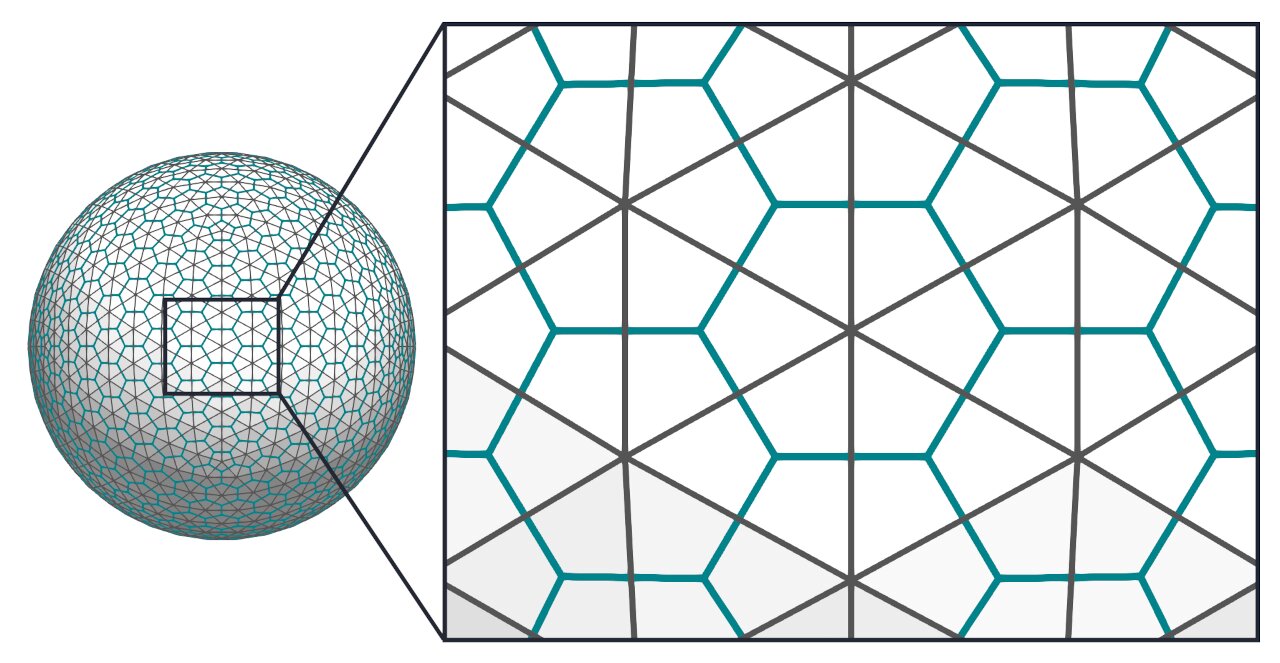
Illustration of the concept of a dual mesh.

The original mesh is a triangle mesh of a sphere, edges shown in dark gray. The edges of the dual mesh are highlighted in teal. Each vertex of the dual mesh corresponds to a face in the original mesh; each vertex of the original mesh corresponds to a polygonal face in the dual mesh. Note that computing the dual also is a practical way to convert a triangle mesh into an general polygon mesh. Here is how you can compute the dual:

void dual(SurfaceMesh& mesh)
{
  // the new dual mesh
  SurfaceMesh tmp;

  // a property to remember new vertices per face
  auto fvertex = mesh.add_face_property<Vertex>("f:vertex");

  // for each face add the centroid to the dual mesh
  for (auto f : mesh.faces())
    fvertex[f] = tmp.add_vertex(centroid(mesh, f));

  // add new face for each vertex
  for (auto v : mesh.vertices()) {
    std::vector<Vertex> vertices;
    for (auto f : mesh.faces(v))
      vertices.push_back(fvertex[f]);

    tmp.add_face(vertices);
  }

  // swap old and new meshes, don't copy properties
  mesh.assign(tmp);
}

Admittedly, this code is a little more specific to the PMP library. I’m using the centroid() function to compute the center of a face. Here’s the definition:

Point centroid(const SurfaceMesh& mesh, Face f)
{
  Point c(0, 0, 0);
  Scalar n(0);
  for (auto v : mesh.vertices(f)) {
    c += mesh.position(v);
    ++n;
  }
  c /= n;
  return c;
}

I am also using the built-in property mechanism to attach data to mesh entities (mesh.add_face_property...). Here, I’m storing and retrieving the vertices added to the dual mesh. If you want to keep it simple, you can also use a std::vector for managing this information.

I’m also using two frequently used operations when working with meshes:

I’m using iterators to go through all mesh entities (faces, vertices)
I’m using a circulator to traverse all faces incident to a vertex.

The circulator is in the for (auto f : mesh.faces(v)) part. If you are using a different data structure, you need to figure out how to do this for yourself. Check the API documentation of your library. Or just switch to PMP!

The Octahedron

With the new function to compute the dual mesh in place, we have all it takes to generate another Platonic solid. The octahedron is the dual polyhedron of the hexahedron, which we can already generate using the hexahedron() function. All that’s left is to combine the two:

SurfaceMesh octahedron()
{
  auto mesh = hexahedron();
  dual(mesh);
  return mesh;
}

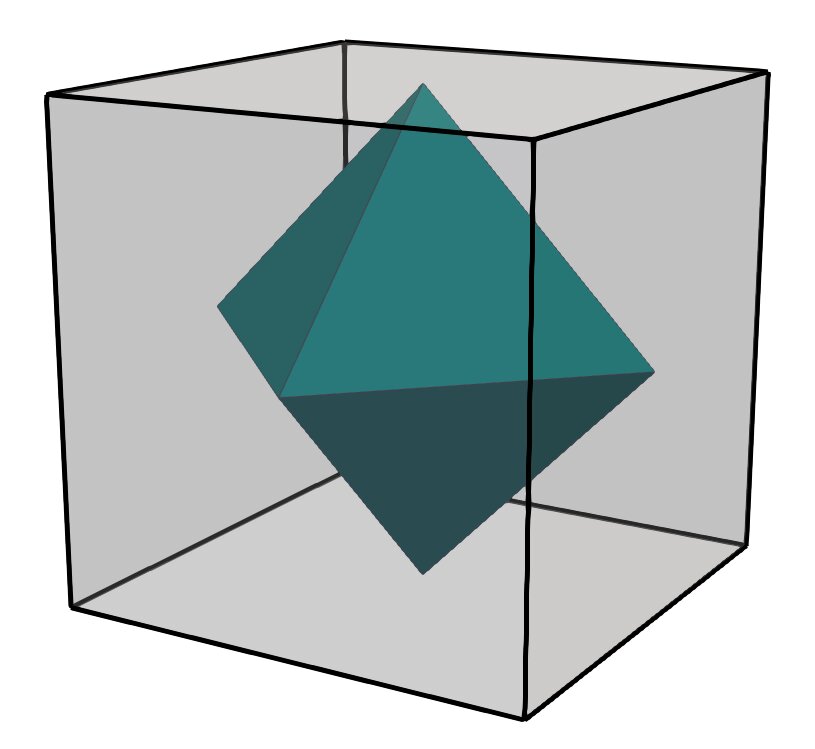
Now that’s a function to my liking: Create something, do something, and return the result. As simple and clear as it gets. Comparing the original hexahedron and the dual octahedron shows that there is an issue, though: The dual mesh is much smaller and inside the original hexahedron.

The dual octahedron contained in the original hexahedron

Normalizing Positions on the Unit Sphere

For the functions defined so far, I took care to compute the vertex coordinates in such a way that they are on the unit sphere. It would be nice to have the same property for the dual meshes as well. A simple solution is to project the vertices of the dual mesh back to the unit sphere. Here’s a function for doing exactly that:

void project_to_unit_sphere(SurfaceMesh& mesh)
{
  for (auto v : mesh.vertices()) {
    auto p = mesh.position(v);
    auto n = norm(p);
    mesh.position(v) = (1.0 / n) * p;
  }
}

Now let’s use this in our function generating the octahedron:

SurfaceMesh octahedron()
{
  auto mesh = hexahedron();
  dual(mesh);
  project_to_unit_sphere(mesh);
  return mesh;
}

And this is what the result looks like:

Octahedron and hexahedron within a sphere

Much better. The two shapes have all their points nicely aligned on the unit sphere, just as we want them to be.

Icosahedron and Dodecahedron

Finally, let’s tackle the remaining two polyhedra, icosahedron and dodecahedron. The two are dual to another, so we only need to generate one of them by hand and then compute the other one using the dual() function. I’m choosing the icosahedron for the manual implementation:

SurfaceMesh icosahedron()
{
  SurfaceMesh mesh;

  float phi = (1.0f + sqrt(5.0f)) * 0.5f; // golden ratio
  float a = 1.0f;
  float b = 1.0f / phi;

  // add vertices
  auto v1  = mesh.add_vertex(Point(0, b, -a));
  auto v2  = mesh.add_vertex(Point(b, a, 0));
  auto v3  = mesh.add_vertex(Point(-b, a, 0));
  auto v4  = mesh.add_vertex(Point(0, b, a));
  auto v5  = mesh.add_vertex(Point(0, -b, a));
  auto v6  = mesh.add_vertex(Point(-a, 0, b));
  auto v7  = mesh.add_vertex(Point(0, -b, -a));
  auto v8  = mesh.add_vertex(Point(a, 0, -b));
  auto v9  = mesh.add_vertex(Point(a, 0, b));
  auto v10 = mesh.add_vertex(Point(-a, 0, -b));
  auto v11 = mesh.add_vertex(Point(b, -a, 0));
  auto v12 = mesh.add_vertex(Point(-b, -a, 0));

  project_to_unit_sphere(mesh);

  // add triangles
  mesh.add_triangle(v3, v2, v1);
  mesh.add_triangle(v2, v3, v4);
  mesh.add_triangle(v6, v5, v4);
  mesh.add_triangle(v5, v9, v4);
  mesh.add_triangle(v8, v7, v1);
  mesh.add_triangle(v7, v10, v1);
  mesh.add_triangle(v12, v11, v5);
  mesh.add_triangle(v11, v12, v7);
  mesh.add_triangle(v10, v6, v3);
  mesh.add_triangle(v6, v10, v12);
  mesh.add_triangle(v9, v8, v2);
  mesh.add_triangle(v8, v9, v11);
  mesh.add_triangle(v3, v6, v4);
  mesh.add_triangle(v9, v2, v4);
  mesh.add_triangle(v10, v3, v1);
  mesh.add_triangle(v2, v8, v1);
  mesh.add_triangle(v12, v10, v7);
  mesh.add_triangle(v8, v11, v7);
  mesh.add_triangle(v6, v12, v5);
  mesh.add_triangle(v11, v9, v5);

  return mesh;
}

Computing the dodecahedron now is straightforward:

SurfaceMesh dodecahedron()
{
  auto mesh = icosahedron();
  dual(mesh);
  project_to_unit_sphere(mesh);
  return mesh;
}

And here is the result showing both the icosahedron and dodecahedron enclosed by the unit sphere:

Icosahedron and dodecahedron within the unit sphere

Wrapping Up

Alright, that’s it for the moment. I hope this was useful to you. The full code is available as well. I’ll eventually write more articles like this one, so stay tuned.

In the meantime, tell me what you think. Comments? Questions? Suggestions? Drop me a mail.

Thanks to u/lycium on Reddit for suggesting a simplification of the icosahedron() function.